Sudoku Solver AR Part 7: Canny Part 2 (Sobel)
This post is part of a series where I explain how to build an augmented reality Sudoku solver. All of the image processing and computer vision is done from scratch. See the first post for a complete list of topics.
The second part of the Canny algorithm involves finding the gradient at each pixel in the image. This gradient is just a vector describing the relative change in intensity between pixels. Since a vector has a magnitude and a direction, then this gradient describes how much the intensity is changing and in what direction.
The gradient is found using the Sobel operator. The Sobel operator uses two convolutions to measure the rate of change in intensity using surrounding pixels. If you studied Calculus, it’s worth noting that this is just a form of differentiation. One convolution measures the horizontal direction and the other measures the vertical direction. These two values together form the gradient vector. Below are the most common Sobel kernels. Unlike the Gaussian kernel, the Sobel kernels do not change so they can simply be hard coded.
`K_x = [[-1,0,1],[-2,0,2],[-1,0,1]]`
`K_y = [[-1,-2,-1],[0,0,0],[1,2,1]]`
Where `K_x` is the horizontal kernel and `K_y` is the vertical kernel.
A little more processing is needed to make the gradient usable for the Canny algorithm. If you’ve studied linear algebra or are familiar with polar coordinates the following should be familiar to you.
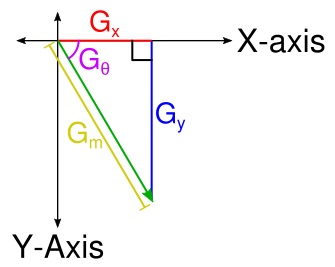
First, the magnitude is needed which describes how quickly the intensity of the pixels are changing. By noting that the result of each convolution describes a change along the x- and y-axis, these two pairs put together form the adjacent and opposite sides of a right triangle. From there it should follow immediately that the magnitude is the length of the hypotenuse and can be solved using Pythagorean theorem.
`G_m = sqrt(G_x^2 + G_y^2)`
Where `G_m` is the magnitude, `G_x` is the result of the horizontal convolution, and `G_y` is the result of the vertical convolution.
The direction of the gradient in radians is also needed. Using a little trigonometry and the fact that we can calculate the tangent using the `G_x` and `G_y` components
`tan(G_theta) = G_y / G_x`
`G_theta = arctan(G_y / G_x)`
Where `G_theta` is the angle in radians. The `arctan` term requires special handling to prevent a divide by zero. Luckily, C++ (and most programming languages) have a convenient atan2 function that handles this case by conveniently returning `+-0` or `+-pi`. The C++ variant of atan2 produces radians in the range `[-pi,pi]` with `0` pointing down the positive x-axis and the angle proceeding in a clockwise direction.
The following example demonstrates how to calculate the gradient for a region of pixels. A typical unsigned 8-bit data type is assumed with the black pixels having a value of 0 and the white pixels having a value of 255.

`P = [[255,255,255],[255,0,0],[0,0,0]]`
`G_x = P ** K_x = (255 * -1) + (255 * 0) + (255 * 1) + (255 * -2) + (0 * 0) + (0 * 2) + (0 * -1) + (0 * 0) + (0 * 1) = -510`
`G_y = P ** K_y = (255 * -1) + (255 * -2) + (255 * -1) + (255 * 0) + (0 * 0) + (0 * 0) + (0 * 1) + (0 * 2) + (0 * 1) = -1020`
`G_m = sqrt((-510)^2 + (-1020)^2) = 1140.39467`
`G_theta = arctan((-1020)/-510) = -2.03444 text{ radians} = 4.24888 text{ radians}`
Here’s an implementation in code that, once again, ignores the border where the convolution would access out of bounds pixels.
const Image image; //Input RGB greyscale image
//(Red, green, and blue channels are assumed identical).
std::vector<float> gradient(image.width * image.height * 2,0.0f); //Output gradient with
//magnitude and angle
//interleaved.
//Images smaller than the Sobel kernel are not supported.
if(image.width < 3 || image.height < 3)
return;
//Number of items that make up a row of pixels.
const unsigned int rowSpan = image.width * 3;
//Calculate the gradient using the Sobel operator for each non-border pixel.
for(unsigned int y = 1;y < image.height - 1;y++)
{
for(unsigned int x = 1;x < image.width - 1;x++)
{
const unsigned int inputIndex = (y * image.width + x) * 3;
//Apply the horizontal Sobel kernel.
const float gx =
static_cast<float>(image.data[inputIndex - rowSpan - 3]) * -1.0f + //Top left
static_cast<float>(image.data[inputIndex - rowSpan + 3]) * 1.0f + //Top right
static_cast<float>(image.data[inputIndex - 3]) * -2.0f + //Mid left
static_cast<float>(image.data[inputIndex + 3]) * 2.0f + //Mid right
static_cast<float>(image.data[inputIndex + rowSpan - 3]) * -1.0f + //Bot left
static_cast<float>(image.data[inputIndex + rowSpan + 3]) * 1.0f; //Bot right
//Apply the vertical Sobel kernel.
const float gy =
static_cast<float>(image.data[inputIndex - rowSpan - 3]) * -1.0f + //Top left
static_cast<float>(image.data[inputIndex - rowSpan]) * -2.0f + //Top mid
static_cast<float>(image.data[inputIndex - rowSpan + 3]) * -1.0f + //Top right
static_cast<float>(image.data[inputIndex + rowSpan - 3]) * 1.0f + //Bot left
static_cast<float>(image.data[inputIndex + rowSpan]) * 2.0f + //Bot mid
static_cast<float>(image.data[inputIndex + rowSpan + 3]) * 1.0f; //Bot right
//Convert gradient from Cartesian to polar coordinates.
const float magnitude = hypotf(gx,gy); //Computes sqrt(gx*gx + gy*gy).
const float angle = atan2f(gy,gx);
const unsigned int outputIndex = (y * image.width + x) * 2;
gradient[outputIndex + 0] = magnitude;
gradient[outputIndex + 1] = angle;
}
}Next is another step in the Canny algorithm which uses the gradient created here to build an image with lines where edges were detected in the original image.
